实验报告
编写一个程序，实现二叉树的各种运算，并在此基础上设计一个程序完成如下功能：
（1）创建一棵二叉树（用键盘按照先序遍历序列输入一个字符串生成二叉树）；
（2）输出前序、中序、后序遍历的遍历序列；
（3）统计并输出二叉树的的结点个数；
（4）输出二叉树的叶子结点的个数；(选做)
实验要求：
用键盘输入一个字符串，按照满二叉树的特点生成一棵二叉树。
测试用例要求：
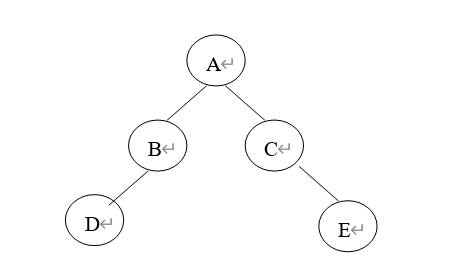
如下二叉树的输入字符串为：ABD###C#E##
书写方法：碰到#说明该二叉树是一棵空树，注意分配（下面缺两个左右补两个#，缺一个左/右子树，补一个#）
二叉链表的结点类型（C++）：
Typedef structure tnode{
int data;
structure tnode *lchild, *rchild;
}bitree,*bitlink ;
实验代码
用上面的二叉树作为例子：
#include<bits/stdc++.h>
using namespace std;
typedef int Status;
typedef char TElemType;
#define OVERFLOW -1
#define ERROR 0
#define OK 1
char ch;
/**
- 采用二叉链表的存储形式
- /
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
/**
- 创建一棵二叉树
- /
void CreateBiTree(BiTree &T) {
//按先序次序输入二叉树中结点的值，创建二叉链表表示的二叉树T
TElemType ch;
cin>>ch;
if(ch == ‘#’){//递归结束，建空树 T = NULL;
} else { T = new BiTNode;
T->data = ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
}
/**
- 先序遍历
- /
void PreOrderTraverse(BiTree &T)
{//先序遍历二叉树T的递归算法
if(T) //若二叉树非空
{ cout << T->data << " "; //访问根结点
PreOrderTraverse(T->lchild); //中序遍历左子树
PreOrderTraverse(T->rchild); //中序遍历右子树
}
}
/**
- 中序遍历
- /
void InOrderTraverse(BiTree &T) {
if (T) { InOrderTraverse(T->lchild);
cout << T->data << " ";
InOrderTraverse(T->rchild);
}
}
/**
- 后序遍历
- /
void PostOrderTraverse(BiTree &T)
{//后序遍历二叉树T的递归算法
if(T) //若二叉树非空
{ PostOrderTraverse(T->lchild); //中序遍历左子树
PostOrderTraverse(T->rchild); //中序遍历右子树
cout << T->data << " "; //访问根结点
}
}
/**
- 统计二叉树中节点个数
- /
int NodeCount (BiTree &T) {
if (T == NULL) { return 0;
} else { return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
}
}
/**
- 二叉树中叶结点个数
- /
int LeavesCount (BiTree &T) {
if (T == NULL) { return 0;
} else if (T->lchild == NULL && T->rchild == NULL) { return LeavesCount(T->lchild) + LeavesCount(T->rchild) + 1;
}
else { return LeavesCount(T->lchild) + LeavesCount(T->rchild);
}
}
int main() {
BiTree test = new BiTNode;
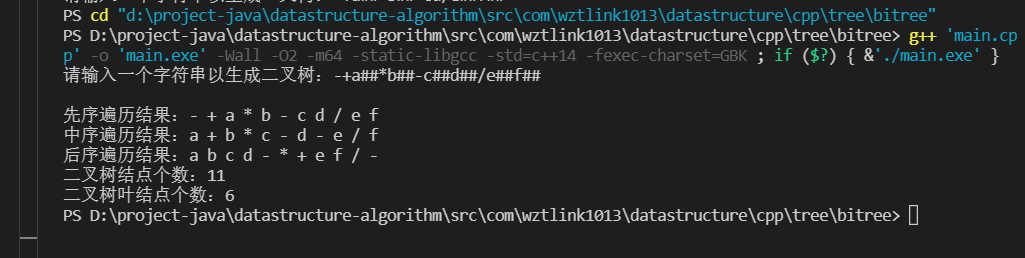
cout << "请输入一个字符串以生成二叉树：";
CreateBiTree(test);
cout <<"\n"<< "先序遍历结果：";
PreOrderTraverse(test);
cout <<"\n"<< "中序遍历结果：";
InOrderTraverse(test);
cout <<"\n"<< "后序遍历结果：";
PostOrderTraverse(test);
cout <<"\n"<< "二叉树结点个数："<<NodeCount(test);
cout <<"\n"<< "二叉树叶结点个数："<<LeavesCount(test);
}
DFS遍历算法
DFS遍历分三种情况：先序、中序、后序
把一颗树遍历完，有下面三种方法：
- 波兰表达式 -> 先序遍历二叉树
- 中缀表达式 -> 中序遍历二叉树
- 逆波兰表达式 -> 后序遍历二叉树
手写例子
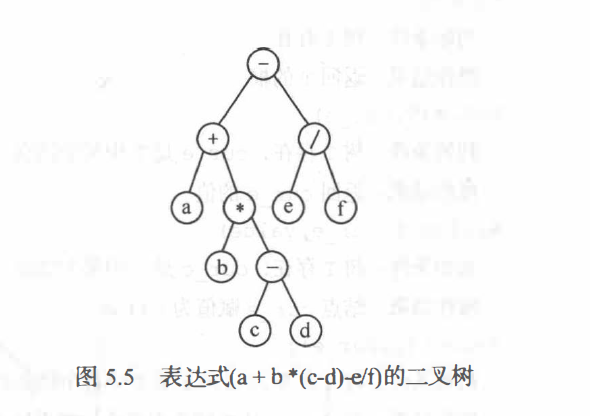
各种遍历结果
- 先序：-+a*b-cd/ef
- 中序：a+b*c-d-e/f
- 后序：abcd-*+ef/-
前序遍历
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function(root) {
let result = []
let preorder = data => {
if (data) {
result.push(data.val)
preorder(data.left)
preorder(data.right)
}
}
preorder(root)
return result
};
中序遍历
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var inorderTraversal = function(root) {
let result = []
let inorder = data => {
if (data) {
inorder(data.left)
result.push(data.val)
inorder(data.right)
}
}
inorder(root)
return result
};
后序遍历
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var postorderTraversal = function(root) {
let result = []
let postorder = data => {
if (data) {
postorder(data.left)
postorder(data.right)
result.push(data.val)
}
}
postorder(root)
return result
};
评论区