前言：数据结构一般就四种关系：集合、线性、树、图。这篇文章打算对图这类数据结构做一个概览。先介绍图的一些术语（复制粘贴：））；然后讲解一下图的各种存储形式；最后把图的应用记录一下，具体应用算法放在算法分类里面。
一、图的一些术语
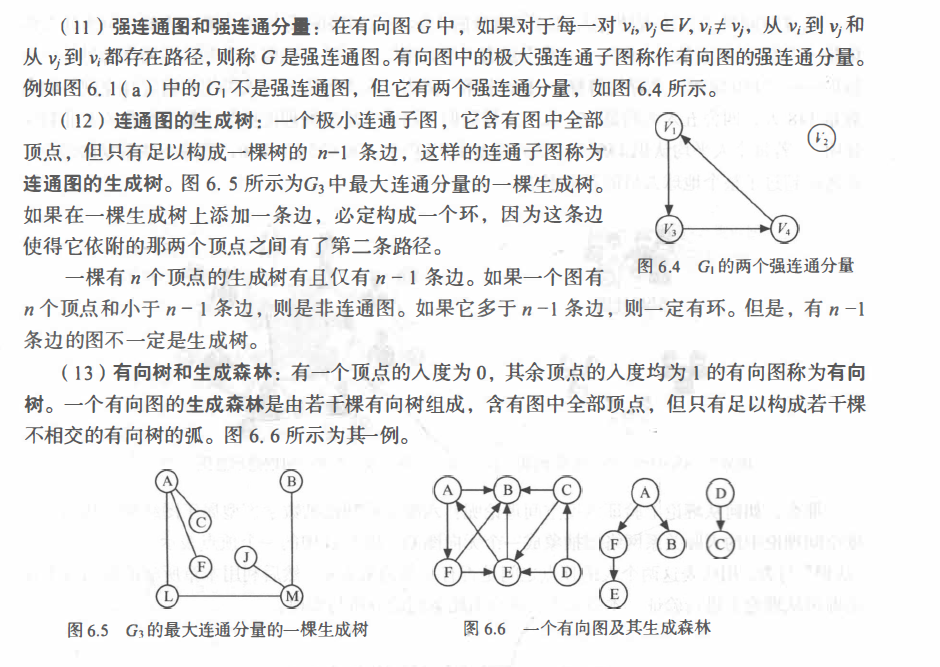
二、图存储
邻接矩阵
创建无向网
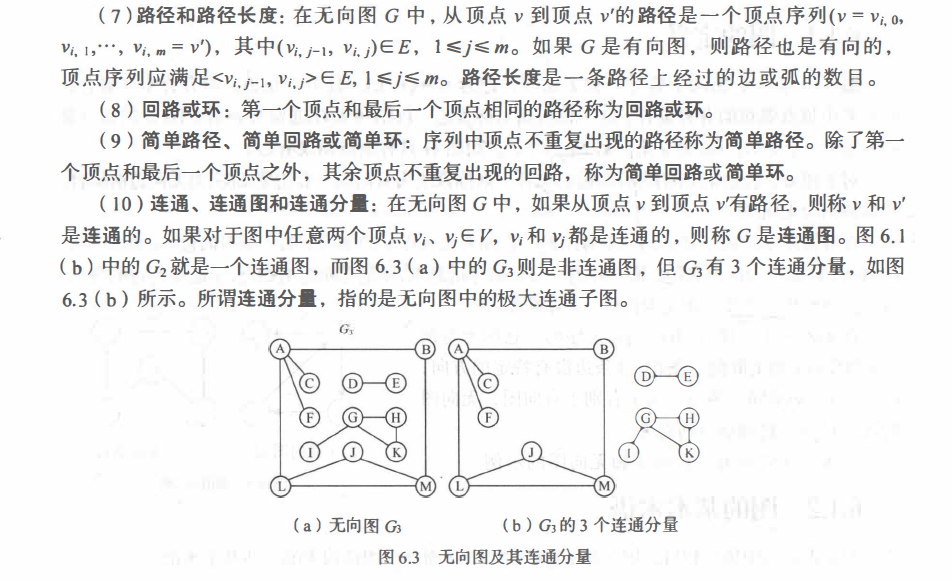
#include<bits/stdc++.h>
using namespace std;
#define MVNum 100
#define MaxInt 32767
typedef char VerTexType;
typedef int ArcType;
/**
- 邻接矩阵存储形式
- /
typedef struct {
/* data */
VerTexType vexs[MVNum]; //顶点表
ArcType arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //图的当前顶点和边数
}AMGraph;
/**
- 确定v在G中的位置，即顶点数组的下标
- /
int LocateVex(AMGraph &G, char v) {
for (int i = 0; i < G.vexnum;i++) { if (v == G.vexs[i]){
return i;
}
}
}
/**
- 创建无向网
- 如果创建无向图
- /
void CreateUDN(AMGraph &G) {
// 采用邻接矩阵表示法，创建无向图G
cout << "请输入顶点数和边数：" << endl;
cin >> G.vexnum >> G.arcnum; //输入顶点数和边数
// 初始化顶点
for (int i = 0; i < G.vexnum;i++){ cout << "请输入第" << i << "个顶点值" << endl;
cin >> G.vexs[i];
}
// 初始化邻接矩阵的边的权值为最大值
for (int i = 0; i < G.vexnum;i++) { for (int j = 0; j < G.vexnum;j++) {
G.arcs[i][j] = MaxInt;
}
}
// 构造邻接矩阵
for (int k = 0; k < G.arcnum;k++) { cout << "请输入每条边所依附的顶点和权值：" << endl;
char v1, v2;
int w; //一条边所依附的顶点和权值
cin >> v1 >> v2 >> w;
int i = LocateVex(G, v1);
int j = LocateVex(G, v2);
G.arcs[i][j] = w;
G.arcs[j][i] = w;
}
}
void Display(AMGraph &G) {
for (int i = 0; i < G.vexnum;i++) {
for (int j = 0; j < G.vexnum;j++) {
cout << G.arcs[i][j] << " ";
}
cout << endl;
}
}
int main() {
AMGraph test;
// CreateUDN(test);
Display(test);
}
创建无向图
对CreateUDN 进行处理：
- G.arcs[i][j] = MaxInt;改为G.arcs[i][j] = 0;
- 将w改为常量1即可
创建有向网
对CreateUDN 进行处理：
- 删除G.arcs[j][i] = w;
创建有向图
对CreateUDN 进行处理：
- 删除G.arcs[j][i] = w;
邻接表
#include <bits/stdc++.h>
using namespace std;
#define MVNum 100
#define MaxInt 32767
typedef char VerTexType;
typedef int OtherInfo;
/**
- 邻接表存储
- /
/**
- 存储结构
- /
typedef struct ArcNode { //边结点
int adjvex; //该边所指向的结点的位置
struct ArcNode *nextarc; //指向下一条边的指针
OtherInfo info; //和边相关的其他信息
}ArcNode;
typedef struct VNode { //顶点信息
VerTexType data; //数据域，存放顶点vi的名称或其他有关信息
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VNode, AdjList[MVNum]; //AdjList表示邻接表的类型
typedef struct {
AdjList vertices;
int vexnum, arcnum; //图当前的顶点数和边数
}ALGragh; //邻接表（Adjacency List）
/**
- 找到v顶点在图中的位置
- /
int LocateVex(ALGragh &G, char v) {
for (int i = 0; i < G.vexnum;i++) { if (v == G.vertices[i].data) {
return i;
}
}
}
/**
- 邻接表创建无向图
- /
void CreateUDG(ALGragh &G) {
cin >> G.vexnum >> G.arcnum; // 邻接表的顶点数和边数
for (int i = 0; i < G.vexnum;i++) { cin >> G.vertices[i].data;
G.vertices[i].firstarc = NULL;
} for (int k = 0; k < G.arcnum;k++) { char v1, v2;
cin >> v1 >> v2;
int i = LocateVex(G, v1);
int j = LocateVex(G, v2);
ArcNode *p1 = new ArcNode;
p1->adjvex = j;
p1->nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc = p1;
ArcNode *p2 = new ArcNode;
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p1;
}
}
有向图：十字链表存储
#include <bits/stdc++.h>
using namespace std;
typedef int Status;
#define OK 1;
//—-有向图的十字链表储存表示—-
#define MAX_VERTEX_NUM 20
typedef char VerTexType;
typedef int InfoType;
typedef struct ArcBox
{
int tailvex, headvex; //该弧的头尾和头顶点的位置
struct ArcBox *hlink, *tlink; //分别为弧头相同和弧尾相同的链域
InfoType *info; //该弧相关信息的指针
}ArcBox;
typedef struct VexNode
{
VerTexType data;
ArcBox *firstin, *firstout; //分别指向该顶点的第一项入弧和出弧
}VexNode;
typedef struct
{
VexNode xlist[MAX_VERTEX_NUM]; //表头向量
int vexnum, arcnum; //有向图的当前顶点数和弧数
}OLGraph; //十字链表（Orthogonal List）
无向图：邻接多重表存储
#include <bits/stdc++.h>
using namespace std;
typedef int Status;
#define OK 1;
//—-无向图的邻接多重表储存表示—-
#define MAX_VERTEX_NUM 20
typedef char VerTexType;
typedef int InfoType;
typedef enum
{
unvisited, visited //枚举unvisited是0，visited是1，注意没有分号
}VisitIf;
typedef struct EBox
{
VisitIf mark; //访问标记
int ivex, jvex; //该边依附的两个顶点的位置
struct EBox *ilink, *jlink; //分别指向依附这两个顶点的下一条边
InfoType *info; //该边的信息指针
}EBox;
typedef struct VexBox
{
VerTexType data;
EBox *firstedge; //指向第一条依附该顶点的边
}VexBox;
typedef struct
{
VexBox adjmulist[MAX_VERTEX_NUM];
int vexnum, arcnum; //无向图当前的顶点数和边数
}AMLGraph; //邻接多重表(Adjacency Multilist)
其他：边集数组
其他：链式前向星
三、图的应用
- 最小生成树
- 最短路径
- 环路
- 关键路径
具体这几类问题都是算法中的贪心算法所属，故将其放到算法分类里面了。
评论区